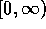Markov-keten met continue tijd-parameter

Het verschil met de in de vorige paragraaf behandelde Markov-keten is in de tijd-parameter. Hier is de tijd-parameter een continue grootheid. Het is een element van de positieve reële rechte .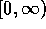

Bij Markov-ketens (continue of discrete tijd-parameter) is de toestandsruimte altijd discreet. Mogelijke toestandruimtes van Markov-ketens zijn bijvoorbeeld:

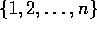
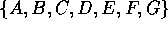
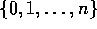
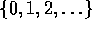
In de rest van dit hoofdstuk zullen we steeds uitgaan van een toestandsruimte die begint bij ``0''. Dus één van de laatste twee genoemde mogelijke toestandsruimtes.

Omdat hier de tijd-parameter continu is, houden we veranderingen bij van de Markov-keten in infinitesimale tijdsintervalletjes. Het is daarom niet onredelijk om de aandacht te beperken tot die Markov-processen waarbij de toestandsovergangen alleen plaatsvinden naar buur-toestanden. Markov-processen waarbij alleen overgangen plaatsvinden naar buur-toestanden worden geboorte-sterfte processen genoemd.

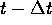
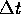
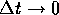
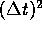
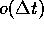
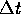
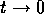
Voor een geboorte-sterfte proces zijn de overgangskansen van de toestand op tijdstip naar een toestand op tijdstip t hieronder gegeven. Beschouw als een klein getal, later beschouwen we de limiet . Termen van de orde en hoger zijn daarom hieronder samengevat als , wat wil zeggen dat deze termen ten opzichte van verwaarloosd kunnen worden als .

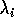
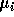
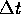
Hierin is de geboorte-intensiteit in toestand i en de sterfte-intensiteit in toestand i. Zo'n intensiteit stelt, na vermenigvuldiging met , de kans voor op een overgang naar een toestand met één meer of één minder.

Als voorheen definiëren we

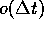
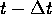
De kans dat het proces op tijdstip t in toestand i is wordt, op termen van de orde na, volledig bepaald door de kans dat het op tijdstip in toestand i-1, i of i+1 was:

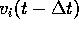
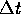
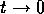
Uit bovenstaande vergelijking kunnen we de afgeleide bepalen van de kans om in toestand i te zijn, door de term naar het linkerlid te brengen, te delen door , en dan de limiet te nemen:

Merk op dat als de index i=0 is, dan valt de eerste term van het rechterlid weg. Ook is in die toestand de sterfte intensiteit 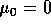. We krijgen dan voor i=0:

In het geval van een continue-tijd Markov-keten met een eindige toestandsruimte 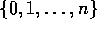, geldt dat n = 0 en krijgen we een soortgelijke aanpassing van de differentiaalvergelijking (4.47).

De differentiaalvergelijkingen (4.47) kunnen weer compact opgeschreven worden in matrixnotatie. We definiëren daartoe de volgende tri-diagonale matrix Q. Deze matrix wordt de infinitesimaalgenerator van de Markov-keten genoemd.

De differentiaalvergelijking voor 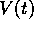, de kansverdeling op tijdstip t, wordt dan een gewone eerste orde lineaire differentiaalvergelijking.

In veel gevallen is men geïnteresseerd in de evenwichtsverdeling van de continue-tijd Markov-keten. De berekening daarvan wordt weer even eenvoudig als dat was voor een discrete-tijd Markov-keten met alleen overgangen naar buurtoestanden. Dat behandelen we aan het eind van dit hoofdstuk.

Eerst gaan we nog in op het tijdsafhankelijke gedrag van de kansverdeling (de oplossing van de differentiaalvergelijking (4.50)). Dit vraagt iets meer geavanceerde begrippen uit de matrixrekening. Voorbeeld 4.5 laat een toepassing zien waar het nodig is om de vector 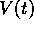als functie van t te berekenen.

De oplossing van (4.50) wordt gegeven door:

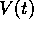
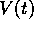
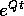
In het geval dat en Q gewoon scalaire grootheden zijn (gewone getallen, en niet een vector en een matrix), is het niet zo moeilijk om te verifiëren dat aan (4.50) voldoet. In het vector matrix geval is (4.52) evenzo de oplossing van (4.50), maar dan moeten we nog wel even aangeven hoe gedefinieerd is. Deze definitie gaat met behulp van de reeksontwikkeling van de e-macht:

I stelt de eenheidsmatrix voor (1-en op de diagonaal en verder 0-en). Het berekenen van machten van matrices hebben we al gezien aan het begin van dit hoofdstuk. Het vermenigvuldigen van een matrix met een scalar (bijvoorbeeld t of 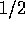) betekent het vermenigvuldigen van elk matrixelement met die scalar. Het optellen van matrices is niets anders dan het optellen van de overeenkomstige elementen.

Het is natuurlijk onbegonnen werk, om alle machten van Q uit te rekenen. Om toch verder te kunnen, maken we gebruik van het feit dat Q te diagonaliseren is:

Hierin is U de matrix gevormd door de linker eigenvectoren van Q. D is een diagonaalmatrix, met op de diagonaal de eigenwaarden van Q. Een willekeurige macht van Q is nu te schrijven als:

De n-de macht van een diagonaalmatrix D is direct op te schrijven; dit is de diagonaalmatrix met op de diagonaal de n-de machten van de diagonaalelementen van D.

De reeksontwikkeling (4.53) is nu te schrijven als:

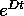
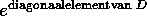
De berekening van vereist geen verdere matrixoperaties, want deze matrix is overal 0, met uitzondering van de diagonaalelementen die gevormd worden door .

We hebben hiermee volledig het tijdsafhankelijke gedrag van de kansverdeling gespecificeerd. Een voorbeeld met een eindige Markov-keten zal de bovenstaande berekeningen verduidelijken.

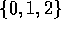
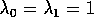
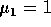
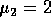
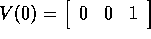
De bezetting van twee telefoonlijnen wordt gemodelleerd als een continue tijd Markov-keten. De toestandsruimte (het aantal bezette lijnen) is . De overgangsintensiteiten zijn en en . De tijdseenheid is de gemiddelde houdtijd van een gesprek. Op t=0 zijn beide lijnen bezet: .

Gevraagd: Hoe groot is de kans dat op 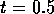beide lijnen nog steeds, of weer opnieuw, bezet zijn? Het antwoord geeft een indicatie voor het instellen van de vertraging voor de automatische oproepherhaler.

De infinitesimaalgenerator Q voor dit voorbeeld is:

Q is te schrijven als 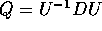. De lezer kan verifiëren dat de rijen van U de linker (eenheids-) eigenvectoren, en de diagonaalelementen van D de eigenwaarden van van Q zijn.

Volgens (4.52) en (4.57) is het verloop van de kansverdeling als functie van t:

Het uitvoeren van bovenstaande matrixvermenigvuldigingen geeft een vector waarvan de elementen een som zijn van een constante term en twee e-machten:

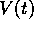
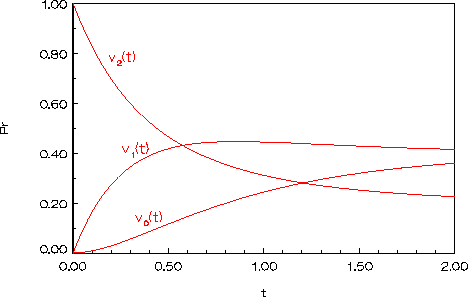
Een grafiek van de drie elementen van is getekend in figuur 4.3.

 
Figuur: Kansverdeling van het aantal bezette lijnen als functie van t, gegeven dat op t=0 beide lijnen bezet zijn.  

Het antwoord op de vraag is:

Dat wil zeggen dat wanneer na een halve gemiddelde houdtijd weer opnieuw gekeken wordt of een lijn vrij is (nadat op t=0 beide lijnen bezet waren) dan is de kans op succes 53%.

De matrixnotatie maakt het eenvoudig om de oplossing van het stelsel differentiaalvergelijkingen op te schrijven. Het voert te ver om daar hier verder op in te gaan. De matrixnotatie komt ook van pas als men de beschikking heeft over routines voor het oplossen van stelsels van lineaire vergelijkingen.

De evenwichtsverdeling

wordt gekenmerkt door het niet meer veranderen (in de tijd gezien) van de kansverdeling, met andere woorden, de waarde van de afgeleide is 0. Dit geeft de volgende verzameling van vergelijkingen voor de evenwichtsverdeling:

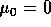
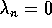
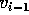
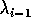
Hierbij is de sterfte-intensiteit in toestand 0 per definitie gelijk aan 0: . Bij een eindige Markov-keten is ook in toestand n de geboorte-intensiteit gelijk aan 0: . Als i=0 is in (4.67) dan moet voor de waarde 0 ingevuld worden. De ongedefinieerde waarde van speelt dan geen rol meer.

Voor het oplossen van de evenwichtsvergelijking moet ook nog gebruik gemaakt worden van de normeringsvergelijking

Evenals het stelsel differentiaalvergelijkingen (4.47), , kan het stelsel evenwichtsvergelijkingen kan in matrixvorm geschreven worden:

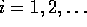
waarin O de nulvector is en Q de infinitesimaalgenerator zoals gedefinieerd in (4.49).

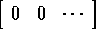
Omdat een geboorte-sterfte proces alleen overgangen tussen buur-toestanden kent, heeft het toestandsdiagram van het Markov-proces een één -dimensionale vorm, en kan de evenwichtsverdeling makkelijk sequentieel uitgerekend worden, zoals verderop zal worden gegeven.

Het toestandsdiagram is weer een praktisch hulpmiddel voor het beschrijven van een geboorte-sterfte proces. De algemene vorm van het toestandsdiagram is getekend in figuur 4.4.

 
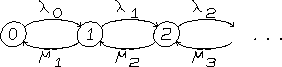
Figuur: Toestandsdiagram van een geboorte-sterfte proces. De waarden langs de pijlen zijn overgangsintensiteiten.  

Het is van belang te realiseren dat de waarden, die langs de pijlen staan van een toestandsdiagram van een continue-tijd Markov-keten, een iets andere interpretatie hebben dan in het geval van een discrete-tijd Markov-keten. In het laatste geval stonden naast de pijlen overgangskansen. In het geval van een continue-tijd Markov-keten zijn die waarden overgangsintensiteiten. Een overgangsintensiteit is: kans per tijdseenheid. 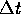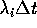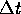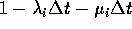Pas na vermenigvuldiging met , heeft bijvoorbeeld de interpretatie van de kans om van toestand i naar i+1 te gaan in een interval van lengte . Daarom staan in een toestandsdiagram van een continue-tijd Markov-keten ook geen pijlen van een toestand naar zichzelf omdat hier geen sprake is van een overgangsintensiteit; wel van een overgangskans die bijvoorbeeld een waarde heeft van , maar dan kan er geen factor t buiten haakjes gehaald worden.

Voor het bepalen van de evenwichtsverdeling van een continue-tijd Markov-keten (als het een geboorte-sterfte proces is) kunnen we hetzelfde algoritme gebruiken als voor discrete-tijd Markov-ketens met een één -dimensionale toestandsruimte. Veel toepassingen van continue-tijd Markov-ketens hebben betrekking op systemen met een oneindige toestandsruimte, bijvoorbeeld wachtrijsystemen met onbegrensde wachtrij-capaciteit. Daarom formuleren we het algoritme voor een oneindige continue-tijd Markov-keten:

Ga uit van een ongenormeerde verdeling W, gedefinieerd door:

Bepaal :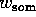

Dan wordt de evenwichtsverdeling V gegeven door: