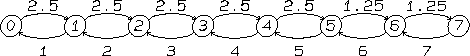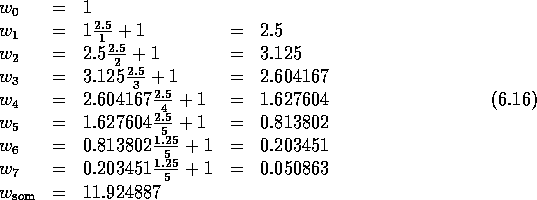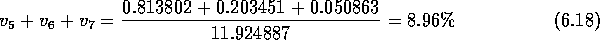Volgende: De Engset-formule
Terug: Markov Verliessystemen
Vorige: Markov Verliessystemen
Voor het dimensioneren van een telefonie bundel is de Erlang-formule
het basisgereedschap. De formule geldt voor elk
verliessysteem met een beperkt aantal loketten (lijnen). De enige
veronderstelling die gemaakt moet worden is dat het aankomstproces
een Poisson-proces is; de bedieningsduur verdeling
(houdtijd van een lijn) kan willekeurig verdeeld zijn.
Er moet wel worden opgemerkt dat de huidige tendens van integratie
van spraak en data, waarbij we virtuele verbindingen hebben,
afbreuk doet aan de algemene toepasbaarheid van de Erlang-formule
als basisgereedschap voor het dimensioneren van een telefonie
bundel. Bij het mengen van virtuele verbindingen met verschillende
karakteristieken wordt het Erlang-model complexer, omdat onder
andere ook rekening gehouden moet worden met het al dan niet
actief zijn van een virtuele verbinding.
Echter het Erlang-model is van toepassing op elk systeem met een
Poisson-aankomstenproces en een beperkt aantal loketten, waarbij
voor ``loketten'' van alles ingevuld kan worden. Het feit dat de
formule niet afhangt van de kansverdeling van de bedieningsduur
heeft in grote mate bijgedragen aan de toepasbaarheid en het
belang van de formule.
Zoals gezegd geldt de Erlang-formule voor een willekeurig 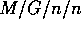 systeem. De formule geeft de kans dat op een willekeurig moment
(en vanwege PASTA voor een willekeurige aankomst) alle n loketten
bezet zijn. De laatste n in
systeem. De formule geeft de kans dat op een willekeurig moment
(en vanwege PASTA voor een willekeurige aankomst) alle n loketten
bezet zijn. De laatste n in 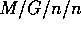 slaat op het aantal plaatsen
in het systeem: dit aantal is gelijk aan het aantal loketten.
Klanten die geen vrij loket vinden (of in telefonie termen:
oproepen die geen vrije lijn vinden) gaan verloren. Daarom heet
dit een verliessysteem. De vijfde parameter is niet vermeld; dit
betekent dat we te maken hebben met een oneindige populatie, wat
weer inhoudt dat het aankomstproces een Poisson-proces is.
slaat op het aantal plaatsen
in het systeem: dit aantal is gelijk aan het aantal loketten.
Klanten die geen vrij loket vinden (of in telefonie termen:
oproepen die geen vrije lijn vinden) gaan verloren. Daarom heet
dit een verliessysteem. De vijfde parameter is niet vermeld; dit
betekent dat we te maken hebben met een oneindige populatie, wat
weer inhoudt dat het aankomstproces een Poisson-proces is.
Voor de berekening van de blokkeringskans (de kans dat alle
loketten bezet zijn) gaan we uit van het 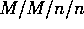 model. Dit model
kan geanalyseerd worden met de inmiddels vertrouwde methode van
het berekenen van de evenwichtsverdeling van een continue-tijd
geboorte-sterfte proces. Het is geen beperking dat we alleen
kijken naar het
model. Dit model
kan geanalyseerd worden met de inmiddels vertrouwde methode van
het berekenen van de evenwichtsverdeling van een continue-tijd
geboorte-sterfte proces. Het is geen beperking dat we alleen
kijken naar het 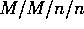 systeem, omdat de evenwichtsverdeling van
het
systeem, omdat de evenwichtsverdeling van
het 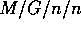 verliessysteem niet afhankelijk is van de
bedieningsduurverdeling. Dit is een opmerkelijk resultaat dat
alleen geldt voor een puur verliessyteem. Dit resultaat kunnen we
hier niet bewijzen.
verliessysteem niet afhankelijk is van de
bedieningsduurverdeling. Dit is een opmerkelijk resultaat dat
alleen geldt voor een puur verliessyteem. Dit resultaat kunnen we
hier niet bewijzen.
Het toestandsdiagram van de continue-tijd Markov-keten is getekend
in figuur 6.1. Hier zien we een constante aankomstintensiteit
van 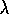 aankomsten per tijdseenheid (gemiddeld) en een
verwerkingsintensiteit die evenredig is met het aantal bezette
lijnen. Een klant heeft een gemiddelde bedieningsduur van
aankomsten per tijdseenheid (gemiddeld) en een
verwerkingsintensiteit die evenredig is met het aantal bezette
lijnen. Een klant heeft een gemiddelde bedieningsduur van 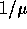 tijdseenheden. In telefonie termen wordt gezegd dat de gemiddelde
houdtijd van een oproep
tijdseenheden. In telefonie termen wordt gezegd dat de gemiddelde
houdtijd van een oproep 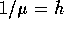 tijdseenheden bedraagt. Het produkt
van het aantal aankomsten per tijdseenheid en de gemiddelde
houdtijd is de hoeveelheid aangeboden verkeer:
tijdseenheden bedraagt. Het produkt
van het aantal aankomsten per tijdseenheid en de gemiddelde
houdtijd is de hoeveelheid aangeboden verkeer:

Het verkeer wordt uitgedrukt in een dimensieloze eenheid die naar
de wiskundige Erlang is genoemd. We zeggen dat het aangeboden
verkeer A Erlang bedraagt.
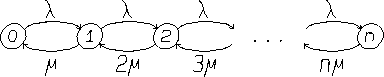
Figuur:
Toestandsdiagram van het 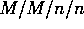 verlies systeem
(Erlang-model).
verlies systeem
(Erlang-model).
Met het bekende recept voor het berekenen van de evenwichts
verdeling, lezen we voor de ongenormeerde kansen 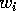 uit het
toestandsdiagram af dat:
uit het
toestandsdiagram af dat:
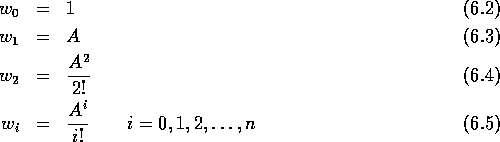
De normeringsconstante is de som van de ongenormeerde kansen:

Waar het ons om gaat, is 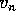 , de kans dat alle lijnen bezet zijn.
Vanwege de eigenschap: Poisson Arrivals See Time Averages (PASTA),
is dit de blokkeringskans voor een oproep. Voor
, de kans dat alle lijnen bezet zijn.
Vanwege de eigenschap: Poisson Arrivals See Time Averages (PASTA),
is dit de blokkeringskans voor een oproep. Voor 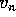 is een hele
reeks van alternatieve notaties in gebruik:
is een hele
reeks van alternatieve notaties in gebruik:
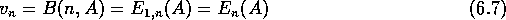
De waarde van 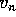 wordt verkregen door
wordt verkregen door 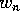 te delen door
te delen door 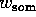 . Dit
geeft de beroemde Erlang B-formule die, uitgeschreven, de volgende
gedaante heeft:
. Dit
geeft de beroemde Erlang B-formule die, uitgeschreven, de volgende
gedaante heeft:
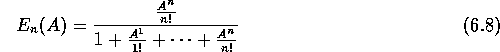
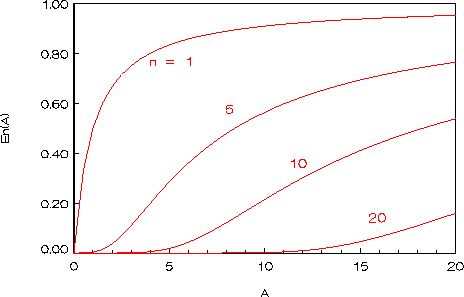
Figuur:
Blokkeringskans volgens het Erlang-model als
functie van het aangeboden verkeer.
Voor het uitrekenen van 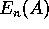 op een programmeerbare rekenmachine
is er een handiger methode dan rechtstreeks via formule (6.8).
Deze methode maakt gebruik van een eenvoudige, recursieve relatie
voor
op een programmeerbare rekenmachine
is er een handiger methode dan rechtstreeks via formule (6.8).
Deze methode maakt gebruik van een eenvoudige, recursieve relatie
voor 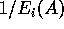 . Definieer:
. Definieer:
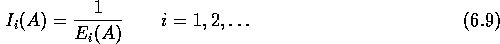
De recursie wordt begonnen door te constateren dat bij 0 lijnen de
blokkeringskans gelijk aan 1 is, dus ook:
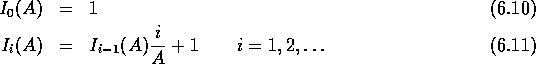

Bij een bedrijf met een PABX (Private Automatic Branch Exchange =
Berijfstelefooncentrale) met vijf buitenlijnen blijkt dat in het
drukke uur de blokkeringskans hoger is dan de gewenste waarde van
1%. Het aangeboden verkeer op de buitenlijnen in het drukke uur
bedraagt 2.5 Erlang.
Gevraagd: Hoe groot is de blokkeringskans en hoeveel lijnen moeten
erbij komen opdat de blokkeringskans kleiner is dan 1%?
De vraag is eenvoudig te beantwoorden met de recursieve relatie
(6.11). Uitgaande van 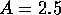 Erlang en
Erlang en 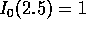 berekenen we
achtereenvolgens
berekenen we
achtereenvolgens
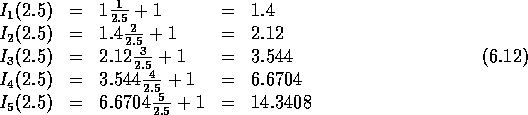
Hieruit volgt direct de blokkeringskans van 2.5 Erlang op 5
lijnen:
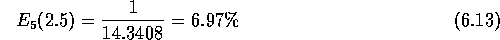
Om te komen tot een blokkeringskans van minder dan 1% moeten we
doorgaan met de recursie totdat de inverse groter is dan 100:
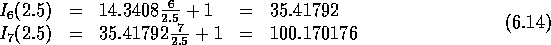
Dus 7 lijnen is voldoende en de blokkeringskans is dan:
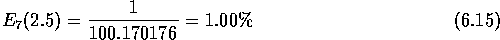

Arie stelt voor om in plaats van twee (dure) buitenlijnen erbij te
nemen, twee wachtplaatsen toe te voegen aan de PABX. Oproepen
vanuit de PABX naar een buitenlijn, die alle buitenlijnen bezet
vinden blijven dan wachten tot een buitenlijn vrij komt. Oproepen
van buiten kunnen niet gebruik maken van de wachtplaatsen. We
gaan, net als in voorbeeld 6.1, uit van 2.5 Erlang aangeboden
verkeer, waarvan de helft gegenereerd wordt door oproepen vanuit
de PABX (de andere helft door oproepen van buiten).
Gevraagd: Hoe groot is de blokkeringskans bij 2.5 Erlang
aangeboden verkeer op 5 lijnen met 2 wachtplaatsen? Geef de
blokkeringskans voor oproepen vanuit de PABX, die gebruik kunnen
maken van de wachtplaatsen, en voor oproepen van buiten?
Het model lijkt op op het  model, maar verschilt doordat
alleen oproepen vanuit de PABX gebruik kunnen maken van de
wachtplaatsen. Het toestands diagram van het aangepaste model is
weergegeven in figuur 6.3:
model, maar verschilt doordat
alleen oproepen vanuit de PABX gebruik kunnen maken van de
wachtplaatsen. Het toestands diagram van het aangepaste model is
weergegeven in figuur 6.3:
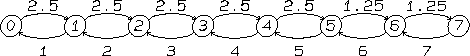
Figuur:
Het toestandsdiagram bij voorbeeld 6.2.
De toestand van het systeem is het aantal klanten dat een lijn
belegd heeft plus eventuele wachtende klanten. De intensiteit
waarmee lijnen vrij komen is gelijk aan het aantal bezette lijnen,
dus nooit groter dan 5 per gemiddelde houdtijd (we kiezen onze
tijdseenheid gelijk aan de gemiddelde houdtijd). Als het systeem
in toestand 5 of 6 is, dan is de overgangsintensiteit naar een
hogere toestand 1.25 per gemiddelde houdtijd, omdat die overgangen
alleen plaatsvinden indien een oproep vanuit de PABX een
wachtplaats bezet.
We berekenen eerst de evenwichts verdeling volgens (4.28)--(4.31)
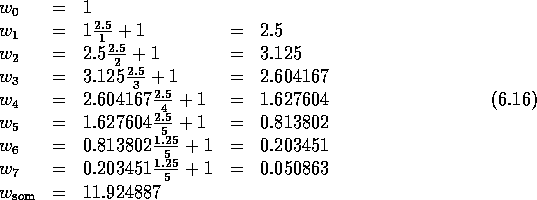
Voor oproepen vanuit de PABX is er alleen blokkering als het
systeem in toestand 7 is. De kans hierop is (slechts):

Voor oproepen van buiten is er blokkering als het systeem in
toestand 5, 6 of 7 is. De kans hierop is:
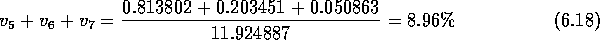




Volgende: De Engset-formule
Terug: Markov Verliessystemen
Vorige: Markov Verliessystemen
Geert A. Awater
Mon Dec 11 15:33:15 MET 1995
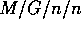 systeem. De formule geeft de kans dat op een willekeurig moment
(en vanwege PASTA voor een willekeurige aankomst) alle n loketten
bezet zijn. De laatste n in
systeem. De formule geeft de kans dat op een willekeurig moment
(en vanwege PASTA voor een willekeurige aankomst) alle n loketten
bezet zijn. De laatste n in 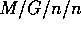 slaat op het aantal plaatsen
in het systeem: dit aantal is gelijk aan het aantal loketten.
Klanten die geen vrij loket vinden (of in telefonie termen:
oproepen die geen vrije lijn vinden) gaan verloren. Daarom heet
dit een verliessysteem. De vijfde parameter is niet vermeld; dit
betekent dat we te maken hebben met een oneindige populatie, wat
weer inhoudt dat het aankomstproces een Poisson-proces is.
slaat op het aantal plaatsen
in het systeem: dit aantal is gelijk aan het aantal loketten.
Klanten die geen vrij loket vinden (of in telefonie termen:
oproepen die geen vrije lijn vinden) gaan verloren. Daarom heet
dit een verliessysteem. De vijfde parameter is niet vermeld; dit
betekent dat we te maken hebben met een oneindige populatie, wat
weer inhoudt dat het aankomstproces een Poisson-proces is.
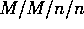 model. Dit model
kan geanalyseerd worden met de inmiddels vertrouwde methode van
het berekenen van de evenwichtsverdeling van een continue-tijd
geboorte-sterfte proces. Het is geen beperking dat we alleen
kijken naar het
model. Dit model
kan geanalyseerd worden met de inmiddels vertrouwde methode van
het berekenen van de evenwichtsverdeling van een continue-tijd
geboorte-sterfte proces. Het is geen beperking dat we alleen
kijken naar het 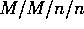 systeem, omdat de evenwichtsverdeling van
het
systeem, omdat de evenwichtsverdeling van
het 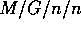 verliessysteem niet afhankelijk is van de
bedieningsduurverdeling. Dit is een opmerkelijk resultaat dat
alleen geldt voor een puur verliessyteem. Dit resultaat kunnen we
hier niet bewijzen.
verliessysteem niet afhankelijk is van de
bedieningsduurverdeling. Dit is een opmerkelijk resultaat dat
alleen geldt voor een puur verliessyteem. Dit resultaat kunnen we
hier niet bewijzen.
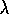 aankomsten per tijdseenheid (gemiddeld) en een
verwerkingsintensiteit die evenredig is met het aantal bezette
lijnen. Een klant heeft een gemiddelde bedieningsduur van
aankomsten per tijdseenheid (gemiddeld) en een
verwerkingsintensiteit die evenredig is met het aantal bezette
lijnen. Een klant heeft een gemiddelde bedieningsduur van 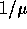 tijdseenheden. In telefonie termen wordt gezegd dat de gemiddelde
houdtijd van een oproep
tijdseenheden. In telefonie termen wordt gezegd dat de gemiddelde
houdtijd van een oproep 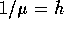 tijdseenheden bedraagt. Het produkt
van het aantal aankomsten per tijdseenheid en de gemiddelde
houdtijd is de hoeveelheid aangeboden verkeer:
tijdseenheden bedraagt. Het produkt
van het aantal aankomsten per tijdseenheid en de gemiddelde
houdtijd is de hoeveelheid aangeboden verkeer:

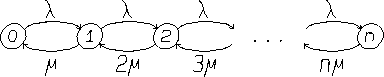
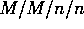 verlies systeem
(Erlang-model).
verlies systeem
(Erlang-model).
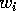 uit het
toestandsdiagram af dat:
uit het
toestandsdiagram af dat:
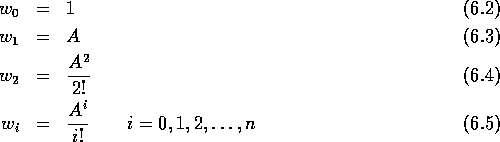

 , de kans dat alle lijnen bezet zijn.
Vanwege de eigenschap: Poisson Arrivals See Time Averages (PASTA),
is dit de blokkeringskans voor een oproep. Voor
, de kans dat alle lijnen bezet zijn.
Vanwege de eigenschap: Poisson Arrivals See Time Averages (PASTA),
is dit de blokkeringskans voor een oproep. Voor 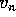 is een hele
reeks van alternatieve notaties in gebruik:
is een hele
reeks van alternatieve notaties in gebruik:
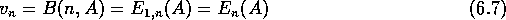
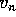 wordt verkregen door
wordt verkregen door 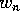 te delen door
te delen door 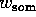 . Dit
geeft de beroemde Erlang B-formule die, uitgeschreven, de volgende
gedaante heeft:
. Dit
geeft de beroemde Erlang B-formule die, uitgeschreven, de volgende
gedaante heeft:
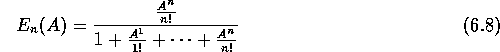

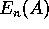 op een programmeerbare rekenmachine
is er een handiger methode dan rechtstreeks via formule (
op een programmeerbare rekenmachine
is er een handiger methode dan rechtstreeks via formule (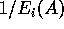 . Definieer:
. Definieer:
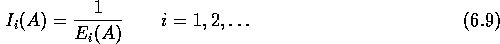
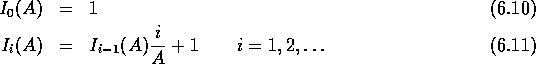

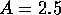 Erlang en
Erlang en 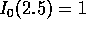 berekenen we
achtereenvolgens
berekenen we
achtereenvolgens
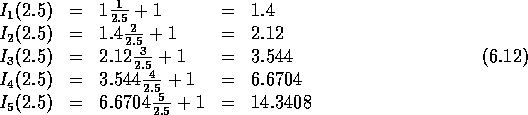
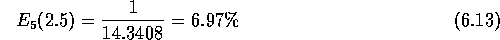
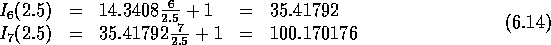
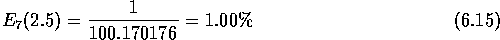

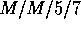 model, maar verschilt doordat
alleen oproepen vanuit de PABX gebruik kunnen maken van de
wachtplaatsen. Het toestands diagram van het aangepaste model is
weergegeven in figuur
model, maar verschilt doordat
alleen oproepen vanuit de PABX gebruik kunnen maken van de
wachtplaatsen. Het toestands diagram van het aangepaste model is
weergegeven in figuur